Structurile anume investigate de matematică își au deseori rădăcinile în științele naturale, cel mai adesea în fizică. Matematica definește și investighează și structuri și teorii proprii, în special pentru a sintetiza și unifica multiple câmpuri matematice sub o teorie unică, o metodă ce facilitează în general metode generice de calcul. Ocazional, matematicienii studiază unele domenii ale matematicii strict pentru interesul abstract exercitat de acestea, ceea ce le transformă într-o abordare mai degrabă legată de artă decât de știință.
Din punct de vedere istoric, ramurile majore ale matematicii au derivat din necesitatea de a face calcule comerciale, de a măsura terenuri și de a predetermina evenimente astronomice cu scopuri agriculturale. Aceste domenii specifice pot fi folosite pentru a delimita în mod generic tendințele matematicii până în ziua de astăzi, în sensul delimitării a trei tendințe specifice: studiul structurii, spațiului și al schimbărilor.
Studiul structurii se bazează în mod generic pe teoria numerelor: inițial studiul numerelor naturale, numere pare, numere impare apoi numere întregi, continuând cu numere raționale și în sfârșit numere reale, întotdeauna corelate cu operațiile aritmetice între acestea, toate acestea făcând parte din algebra elementară. Investigarea în profunzime a acestor teorii și abstractizarea lor a dus în final la algebra abstractă care studiază printre altele inele și corpuri, structuri care generalizează proprietățile numerelor în sensul obișnuit. Conceptul indispensabil în fizică de vector, generalizat în sensul de spațiu vectorial și studiat în algebra lineară este comun studiului structurii și studiului spațiului.
Studiul spațiului pornește în mod natural de la geometrie, începând de la geometria euclidiană și trigonometria familiară în trei dimensiuni și generalizată apoi la geometrie neeuclidiană, care joacă un rol esențial în teoria relativității. O mulțime de teorii legate de posibilitatea unor construcții folosind rigla și compasul au fost încheiate de teoria Galois. Ramurile moderne ale geometriei diferențiale și geometriei algebrice abstractizează studiul geometriei în direcții distincte: geometria diferențială accentuează uzul sistemului de coordonate și al direcției, pe când geometria algebrică definește obiectele mai degrabă ca soluții la diverse ecuații polinomiale. Teoria grupurilor investighează conceptul de simetrie în mod abstract, făcând legătura între studiul structurii și al spațiului. Topologia face legătura între studiul spațiului și studiul schimbărilor, punând accent pe conceptul continuității.
Studiul schimbării este o necesitate mai ales în cazul științelor naturale, unde măsurarea și predicția modificărilor unor variabile este esențială. Calculul diferențial a fost creat pentru acest scop, pornind de la definiția relativ naturală a funcțiilor dintre diverse dimensiuni și rata lor de schimbare în timp, metodele de rezolvare ale acestora fiind ecuațiile diferențiale. Din considerente practice, este convenabil să se folosească numerele complexe în această ramură.
O ramură importantă a matematicii aplicate este statistica, aceasta utilizând teoria probabilității care facilitează definirea, analiza și predicția a diverse fenomene, și care este folosită într-o multitudine de domenii.
Cuprins[ascunde] |
[modificare] Etimologie
Cuvântul matematică își are originea în cuvântul grecesc μάθημα máthēma, care însemna „învățare”, „studiu”, „știință”, la rândul lui provenind din verbul manthanein, „a învăța”.[1] Termenul mathema a căpătat încă din perioada clasică și sensul precis de „studiu matematic”. Adjectivul corespunzător este μαθηματικός mathēmatikós, însemnând „legat de învățare” sau „studios”, iar mai târziu, „matematic”. Din greacă, termenii au fost preluați în latină, unde științele matematice, numite în grecește μαθηματικὴ τέχνη mathēmatikḗ tékhnē, au fost denumite cu pluralul ars mathematica.Din latină, termenul mathematica a fost preluat în forme asemănătoare în toate limbile europene moderne. Forma aparentă de plural din engleză, ca și pluralul franțuzesc les mathématiques, au revenit în latină sub forma pluralului neutru mathematica (Cicero), pornind de la pluralul grecesc τα μαθηματικά ta mathēmatiká, acesta fiind utilizat de Aristotel cu sensul de „toate lucrurile matematice”.
În română, termenul a fost copiat după franțuzescul mathématique și italienescul matematica.[2].
[modificare] Istorie
Articol principal: Istoria matematicii.
Este posibil ca oamenii să-și fi dezvoltat anumite abilități matematice încă înainte de apariția scrierii. Cel mai vechi obiect care dovedește existența unei metode de calcul este osul din Ishango, descoperit de arheologul belgian Jean de Heinzelin de Braucourt în regiunea Ishango din Republica Democrată Congo, care datează din 20.000 înaintea erei noastre[3][4][5]. Dezvoltarea matematicii, ca bagaj de cunoștințe transmis de-a lungul generațiilor, în primele civilizații, este legată strict de aplicațiile sale concrete: comerțul, gestiunea recoltelor, măsurarea suprafețelor, predicția evenimentelor astronomice și, câteodată, de ritualurile religioase. Aceste nevoi au dus la împărțirea matematicii în ramuri ce se ocupau cu studiul cantității, structurii și spațiului.Primele descoperiri matematice țin de extragerea rădăcinii pătrate, a rădăcinii cubice, rezolvarea unor ecuații polinomiale, trigonometrie, fracții, aritmetica numerelor naturale etc. Acestea au apărut în cadrul civilizațiilor akkadiene, babyloniene, egiptene, chineze și civilizațiile de pe valea Indului.
În Grecia antică, matematica, influențată de lucrările anterioare și de specificațiile filosofice, generează un grad mai mare de abstractizare. Noțiunile de demonstrație și de axiomă apar în această perioadă. Apar două ramuri ale matematicii, aritmetica și geometria. În secolul al III-lea î.Hr., Elementele lui Euclid[6] rezumă și pun în ordine cunoștințele matematice ale Greciei antice.

O pagină a tratatului de la Al-Khawarizmi
În timpul Renașterii, o parte din textele arabe sunt studiate și traduse în latină. Cercetarea matematică se concentrează în Europa. Calculul algebric se dezvoltă ca urmare a lucrărilor lui François Viète și René Descartes. Newton și Leibniz au inventat, independent, calculul infinitezimal.
În secolul al XVIII-lea și secolul al XIX-lea, matematica cunoaște o nouă perioadă de dezvoltare intensă, cu studiul sistematic al structurilor algebrice, începând cu grupurile (Évariste Galois) și inelele (concept introdus de Richard Dedekind).
În secolul al XIX-lea, David Hilbert și Georg Cantor dezvoltă o teorie axiomatică asupra căutării fundamentelor matematice. Această dezvoltare a axiomaticii va conduce în secolul al XX-lea la definirea întregii matematici cu ajutorul unui singur limbaj: logica matematică.
Secolul XX a fost martorul unei specializări a domeniilor matematicii, nașterea și dezvoltarea a numeroase ramuri noi, cum ar fi teoria spectrală, topologii algebrice sau geometrie algebrică. Informatica a avut un puternic impact asupra cercetării. Pe de o parte, a facilitat comunicarea între cercetători și răspândirea descoperirilor, pe de alta, a constituit o unealtă foarte puternică pentru testarea teoriilor.
[modificare] Inspirație, matematică pură și aplicată, estetică
În zilele noastre, toate științele utilizează rezultatele muncii matematicienilor și multe alte domenii sunt generate de matematica însăși. De exemplu, fizicianul Richard Feynman, a inventat formularea mecanicii cuantice sub forma integralelor de drum [7] folosind o combinație între descoperiri de natură matematică, intuiții fizice și teoria stringurilor, o teorie științifică încă în dezvoltare care încearcă să unifice cele 4 forțe fundamentale din natură, continuând să inspire noi ramuri ale matematicii.[8] Unele ramuri ale matematicii sunt singurele relevante pentru domeniile pe care le-au inspirat și se aplică în continuare pentru rezolvarea problemelor viitoare. Adeseori însă, matematica inspirată de către un domeniu s-a dovedit utilă în multe altele și a reunit problematica generală a conceptelor matematice. Faptul remarcabil că chiar și matematica pură se reflectă în aplicații practice este redat de ceea ce Eugene Wigner a numit "eficiența irațională a matematicii"[9]. Ca în multe alte domenii, explozia de cunoștințe din știință a dus la specializări în matematică. O diferență majoră este între matematica pură și matematica aplicată: cei mai mulți matematicieni își fac cercetările separat într-unul din aceste domenii iar alegerea finală este făcută odată cu terminarea studiilor. Câteva domenii din matematica aplicată au fuzionat cu domenii care prin tradiție erau din afara ei și au devenit astfel discipline noi, cum ar fi statistica, cercetarea operațională, și știința calculatoarelor. Cei care au înclinații spre matematică găsesc adesea aspecte estetice în multe domenii din matematică. Mulți matematicieni vorbesc despre eleganța matematicii, despre o estetică intrinsecă și o frumusețe ascunsă. Sunt apreciate simplitatea și generalizarea. Se poate vorbi de frumusețea și eleganța unei demonstrații, cum ar fi cazul demonstrației lui Euclid asupra infinității numerelor prime, a metodei numerice de calcul rapid ca în cazul transformatei rapide Fourier. G. H. Hardy, în „A Mathematician's Apology” își exprima credința că aceste considerații estetice sunt, în ele însele, suficiente pentru a justifica studiul matematicii pure.[10] După Paul Erdős, care ar fi vrut să afle „Cartea” în care Dumnezeu a notat demonstrațiile lui favorite, matematicienii năzuiesc adeseori să găsească demonstrații ale teoremelor care sunt, în special, elegante.[11] [12]) Popularitatea matematicii distractive este un alt indiciu al plăcerii găsite în rezolvarea problemelor de matematică.[modificare] Limbajul matematic
Matematica folosește un limbaj propriu. Anumiți termeni din limbajul curent, cum ar fi grup, inel sau corp pot avea un înțeles diferit în limbajul matematic. Mai des însă, termenii sunt inventați și introduși în funcție de necesități: izomorfism, topologie, iterație, etc. Numărul relativ mare al termenilor noi sau cu înțeles schimbat face ca înțelegerea matematicilor avansate de către nespecialiști să fie dificilă.Limbajul matematic se bazează și pe formule. Acestea conțin anumite simboluri, unele împrumutate din calculul propozițional, cum ar fi implicația logică
 sau operatorul pentru negație
sau operatorul pentru negație , altele în legătură cu calcul cu predicate (simbolurile pentru „oricare ar fi”
, altele în legătură cu calcul cu predicate (simbolurile pentru „oricare ar fi”  și „există”
și „există”  ). Cea mai mare parte din notațiile folosite în prezent au fost introduse după secolul al XVI-lea[13].
). Cea mai mare parte din notațiile folosite în prezent au fost introduse după secolul al XVI-lea[13].Motivul principal pentru care au fost introduse simbolurile și termenii noi îl reprezintă necesitatea exprimării cât mai exacte a ideilor (o caracteristică comună științelor exacte, numită rigoare). Rigoarea este necesară pentru a evita teoremele false, generate de interpretări greșite.
Trebuie subliniat faptul că există și un limbaj matematic (metalimbaj) ce descrie matematica însăși. Acest limbaj este logica.
[modificare] Matematica privită ca știință

Carl Friedrich Gauss, pictură de C.A. Jensen
În latină – Regina Scientiarum, în germană – Königin der Wissenschaften. Ambele expresii sunt legate de cuvântul „știință” care înseamnă (domeniu de) cunoștințe. Într-adevăr, în acest sens, nu există îndoieli că matematica este o știință. Restrângerea sensului de știință doar la domenii specializate care studiază natura nu mai este de actualitate. Dacă ar fi considerate științe doar acele domenii ale cunoașterii care se ocupă strict de lumea fizică, atunci matematica, sau cel puțin matematica pură, ar trebui să nu fie considerată o știință. Albert Einstein spunea că „atunci când legile matematicii se referă la realitate, ele nu sunt sigure iar când sunt sigure, ele nu se referă la realitate” (as far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality) [14]
Mulți filozofi cred că, ne putând fi demonstrată experimental, matematica nu poate fi o știință după definiția dată de Karl Popper. [15] În anii 1930, lucrări importante de logică matematică au arătat că matematica nu poate fi redusă la logică și Karl Popper a tras concluzia că „cele mai multe teorii matematice sunt, ca și cele din fizică și biologie, deductive: ca urmare, matematica pură, în cele din urmă, devine mult mai aproape de științele naturii ale căror ipoteze sunt presupuneri, așa cum s-a observat recent”[16]. Alți gânditori, printre care Imre Lakatos, au afirmat că matematica însăși falsifică realitatea.
Un alt punct de vedere ar fi acela că anumite domenii științifice (cum ar fi fizica teoretică) sunt de fapt științe matematice cu axiome care corespund realității. Cercetătorul în fizică teoretică J. M. Ziman a propus ca științele să fie considerate cunoștințe publice iar matematica să fie inclusă între ele. În orice caz, matematica are multe părți comune cu științele fizice, folosindu-se de studiul logic al unor ipoteze. Intuiția și experimentele au, de asemenea, roluri importante în formularea ipotezelor, atât în matematică, cât și în (alte) științe. Matematica experimentală continuă să capete o importanță tot mai mare între științele matematice, în acest sens, computerizarea și simularea jucând roluri tot mai importante în științe și în matematică, slăbind astfel obiecțiile potrivit cărora matematica nu ar utiliza metode științifice.
În 2002, în cartea sa, „A New Kind of Science”, Stephen Wolfram susținea că matematica computațională merită să fie explorată empiric, ca orice domeniu științific cu toate atributele. Opiniile matematicienilor în această privință sunt diferite. Mulți dintre ei cred că a denumi acest domeniu o știință înseamnă a-i reduce importanța laturii sale estetice și a-i denatura istoria sa în cadrul celor 7 (șapte) arte libere; alții, dimpotrivă, susțin că ignorarea interferențelor cu științele înseamnă a vedea cu un singur ochi deoarece aplicațiile matematicii în științe și inginerie au adus multe inovații în matematică. Într-un fel, aceste puncte de vedere diferite s-au transformat în dezbateri filosofice: dacă matematica a fost și este creată (ca în artă) sau descoperită (ca în știință). A devenit un fapt obișnuit să vezi universități care au incluse secții de Știință și Matematică, arătând în acest fel că aceste două domenii sunt privite ca fiind aliate dar nu identice. În practică, matematicile sunt în general grupate cu științele la nivele grosiere, după care sunt separate pe parcursul specializării. Aceasta este una din chestiunile care fac obiectul filosofiei matematicii.
Premiile în matematică sunt în general ținute separat de echivalentele lor din știință. Cel mai prestigios premiu în matematică este Medalia Fields, stabilit în 1936 și acum acordat odată la 4 (patru) ani. Este adesea considerat, în mod eronat, echivalentul premiilor Nobel pentru științe. Premiul Wolf pentru Matematică, instituit în 1978, recunoaște realizările pentru întreaga viață iar alt mare premiu internațional, Premiul Abel [17], a fost introdus în 2003. Acestea sunt acordate pentru lucrări speciale, care pot fi inovații sau rezolvări ale unor probleme remarcabile dintr-un domeniu anume. O faimoasă listă de 23 de probleme deschise de acest fel, numită „Problemele lui Hilbert”, a fost alcătuită de matematicianul german David Hilbert în 1900. Această listă a devenit celebră printre matematicieni și în cele din urmă nouă dintre ele au fost rezolvate. O listă nouă, intitulată „Problemele pentru premiul mileniului", a fost publicată în 2000. Soluționarea fiecăreia dintre ele aduce un premiu de 1 milion de dolari celui care o rezolvă. Numai una dintre ele (Ipoteza lui Riemann) se regăsește între problemele lui Hilbert.
[modificare] Subiecte
[modificare] Cantitate

Abacul este o metodă simplă de numărare
Pe măsură ce sistemul de numerotație a avansat, numerele întregi au fost considerate un subset al numerelor raționale, care la rândul său sunt conținute de mulțimea numerele reale. Numerele reale sunt folosite la reprezentarea funcțiilor continue. Mai departe avem numerele complexe, urmate de numere hipercomplexe: cuaternion, octonion, etc.
Un alt domeniu de studiu este dimensiunea mulțimilor, care conduce la numerele cardinale și spre un alt concept legat de infinit: numerele alef, care permit o comparație între mulțimi de dimensiune infinită.
[modificare] Spațiu
Studiul spațiului a început cu studiul geometriei, mai exact, al geometriei euclidiene. Trigonometria combină spațiul și numerele și cuprinde cunoscuta teoremă a lui Pitagora. Studiile moderne generalizează teoriile asupra spațiului introducând noțiunea de geometrie neeuclidiană în locul celei de geometrie euclidiană. Geometria neeuclidiană ocupă un rol central în teoria relativității generalizate și topologie. Cantitatea și spațiul au roluri importante în geometria analitică, geometrie diferențială și geometrie algebrică. În cadrul geometriei diferențiale apar conceptele de „fascicul de mătase” ([2]fiber bundle) și calculul spațiilor topologice. Geometria algebrică descrie obiectele geometrice prin intermediul unor seturi de soluții ale ecuațiilor polinomiale, combinând conceptele de cantitate, spațiu și studiul grupurilor topologice, acestea combinând noțiunile de structură și spațiu. Grupurile Lie sunt folosite în studiul spațiului, structurii și schimbării. Topologia are foarte multe ramificații și a fost domeniul din matematică cu cea mai mare dezvoltare în secolul XX, cuprinzând faimoasa conjectură a lui Poicaré și controversata teoremă a celor patru culori, a cărei demonstrație, făcută doar pe calculator, nu a fost făcută încă de om. | 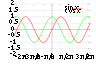 |  |  |  |
| Teorema lui Pitagora | Trigonometrie | Geometrie diferențială | Topologie | Geometrie fractală |
[modificare] Schimbare
Subiecte legate de variația funcțiilor matematice sau de variația numerelor. |  |  |  |  |
| Calcul integral | Calcul vectorial | Ecuații diferențiale | Sisteme dinamice | Teoria haosului |
[modificare] Structură
Multe obiecte matematice, precum mulțimile de numere și funcțiile, au o structură internă. Proprietățile structurale ale acestor obiecte sunt investigate în studiul grupurilor, inelelor, câmpurilor și altor sisteme abstracte, care sunt la rândul lor studiate de algebra abstractă. Un concept important în acest domeniu este cel de vector, generalizat în spații vectoriale. Studiul vectorilor combină trei zone fundamentale ale matematicii: cantitatea, structura și spațiul. Algebra vectorială dezvoltă cercetarea într-o a patra zonă de cercetare fundamentală, cea a schimbării. Un număr de probleme vechi din acest domeniu au fost rezolvate folosind teoria Galois.[modificare] Fundamente și metode
[modificare] Matematici discrete
[modificare] Matematici aplicate
- Mecanică – Analiză numerică – Lingvistica matematică – Optimizare – Poetica matematică– Probabilitate – Statistică – Teoria jocurilor – Biologie matematică – Criptografie – Teoria informației – Dinamica fluidelor
[modificare] Relații spațiale
- Topologie – Geometrie – Trigonometrie – Geometrie algebrică – Geometrie diferențială – Topologie diferențială – Topologie algebrică – Algebră liniară – Geometria fractalilor
[modificare] Teoreme și postulate celebre
- Axioma paralelelor – Teorema lui Pitagora – Cuadratura cercului – Dublarea cubului – Marea teoremă a lui Fermat – Conjectura lui Goldbach – Teorema de incompletitudine a lui Gödel – Conjectura lui Poincaré – Teorema celor patru culori – Lema lui Zorn – Identitatea lui Euler – Conjectura lui Scholz – Teza Church-Turing
[modificare] Teoreme și conjecturi importante
Vezi și Listă de teoreme; Listă de conjecturi.- Ipoteza lui Riemann – Teorema lui Pitagora – Teorema limită centrală – Teorema Gauss-Bonnet – Teorema de factorialitate a lui Gauss
[modificare] Istoria și lumea matematicienilor
[modificare] Vezi și
- Matematicieni
- Medalia Fields
- Tabel de simboluri matematice
- Semne grafice
- Matematica jocurilor de noroc
[modificare] Note
- ^ American Heritage Dictionary of the English Language, mathematical; Online Etymology Dictionary, mathematics
- ^ Dicționarul explicativ al limbii române, 1998, matematică
- ^ fr Bastonul din Ishango - Institut royal des Sciences naturelles de Belgique
- ^ en Osul din Ishango - MathWorld
- ^ fr Les os incisés d'Ishango font naître la numération en Afrique, Le Monde
- ^ en Elementele lui Euclid, sit interactiv
- ^ alte formulări a mecanicii cuantice sunt „formularea matricială”, propusă de Heisenberg, sau formularea sub forma unei ecuații diferențiale, propusă de Schrödinger
- ^ Johnson, Gerald W.; Lapidus, Michel L. (2002). The Feynman Integral and Feynman's Operational Calculus. Oxford University Press
- ^ Eugene Wigner, 1960, "The Unreasonable Effectiveness of Mathematics in the Natural Sciences," Communications on Pure and Applied Mathematics 13(1): 1–14
- ^ Hardy, G. H. (1940). A Mathematician's Apology. Cambridge University Press.
- ^ Gold, Bonnie; Simons, Rogers A. (2008). Proof and Other Dilemmas: Mathematics and Philosophy. MAA
- ^ Aigner, Martin; Ziegler, Gunter M. (2001). Proofs from the Book. Springer
- ^ en Primele apariții ale simbolurilor matematice (Conține mai multe referințe)
- ^ Einstein, p. 28. Citatul este răspunsul lui Einstein la următoarea întrebare: „de ce matematica, un produs al gândirii umane prin excelență, este atât de potrivit pentru studiul realității? El era astfel preocupat de excepționala eficiență a matematicii vis-à-vis de științele naturii.
- ^ Shasha, Dennis Elliot; Lazere, Cathy A. (1998). Out of Their Minds: The Lives and Discoveries of 15 Great Computer Scientists. Springer. p. 228.
- ^ Popper 1995, p. 56
- ^ [1]





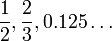
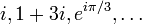









Комментариев нет:
Отправить комментарий